La filosofia nasce come matematica?
Per rispondere alla domanda dobbiamo innanzitutto partire dal significato della parola “filosofia”, amore per la conoscenza, e di conseguenza definire chi è colui che ama la conoscenza, ovvero il filosofo.
La tradizione storica – e mi riferisco alla storia del pensiero umano – ci ha abituati a considerare Pitagora come il primo pensatore che utilizzò la parola “filosofia” in accezione odierna, anche se non tutti gli storici della filosofia sono d’accordo.
Il professor Gabriele Giannantoni sostiene, infatti, che la filosofia nasca con Socrate e che Pitagora sia un sapiente, perché nessuno potrebbe mai mettere in discussione la sua sapienza, ma la filosofia si fonda sul presupposto socratico di “sapere di non sapere”. Di conseguenza, chi è che cerca la conoscenza? – Chi non sa, dunque escludiamo Pitagora che è indubbiamente consapevole di sapere.
Tuttavia, scegliendo di attenerci alla tradizione, Pitagora è il primo filosofo ed essendo il suo pensiero, fondamentalmente matematico, per quanto Pitagora fosse esperto anche nell’arte della medicina, la filosofia nasce perciò come matematica.
La filosofia nasce come matematica?
L’ἀρχή, cioè l’origine del tutto è per i Pitagorici il numero. Sempre considerando che Pitagora non scrisse nulla e che all’interno dei cenacoli pitagorici, come denota K. Popper, la figura stessa di Pitagora venne mitizzata fino a considerarlo a metà tra uomo e Dio, le scoperte pitagoriche nel campo della matematica hanno davvero costituito la base su cui si è sviluppato l’impianto della matematica dei secoli successivi, fino alla prima grande sistematizzazione grazie ad Euclide, allievo di Platone.
La matematica antica era sostanzialmente scissa in aritmetica, la disciplina che studia i numeri e le operazioni di calcolo e geometria, la scienza delle forme nello spazio. Per noi moderni la suddivisione è piuttosto scontata poiché abbiamo di default ereditato i due “a priori” kantiani di spazio e tempo, che associano il primo, cioè lo spazio, alla geometria e il secondo al numero. Lo spazio studia la figura, la superficie delle cose che è qualcosa di continuo, a differenza del numero, correlato fin dal principio al battito del cuore, alla carica che tiene un organismo in vita e dunque ad una percezione discreta.
Ecco che si configura, nella dialettica continuo/discreto, il campo da cui gli antichi hanno astratto la funzione di numero, utilizzato dall’uomo primitivo per il calcolo del bestiame, come testimoniano molti oggetti incisi con tacche regolari che farebbero pensare ad operazioni di computo, anche se, ovviamente, il passaggio dalla tacchetta all’astrazione di numero, ha richiesto un po’ più di tempo in termini di evoluzione e di consapevolezza della specie umana.
La matematica tuttavia non è un’invenzione greca e allora perché si dice che essa nasca con i Pitagorici? La risposta sta nel metodo. E’ ben noto che Caldei, Babilonesi ed Egizi conoscevano il teorema di Pitagora, ad esempio, ma un conto è applicarlo e dare il risultato di un calcolo e ben altro è dimostrare il perché è vero ciò che il teorema enuncia, dove per vero, si intende “una verità” applicabile a tutti gli n triangoli rettangoli sensibili. I Greci dunque dimostravano e per quanto si sia persa la dimostrazione del teorema di Pitagora, da Pitagora enunciata, tanto che per la dimostrazione si fa normalmente riferimento alla proposizione 47 degli “Elementi” di Euclide, i Pitagorici dimostravano di fatto i teoremi, per cui non era importante per loro arrivare al risultato, ma dimostrare come e perché ci si arriva. L’intuizione o visione della mente, che richiama la parola greca “theoria”, da cui teorema, va poi supportata dal ragionamento deduttivo e dall’empiria.
Del resto, oggi è stato riconosciuto, anche nella storia della matematica che le conoscenze matematiche di Pitagora erano per i tempi tutt’altro che ingenue, al punto tale che i Pitagorici non si limitavano allo studio dei soli numeri naturali, ossia gli interi positivi che usiamo per contare e che possono sempre essere rappresentati come rapporto tra numeri a loro volta interi, ma che addirittura i Pitagorici avessero familiarità con gli irrazionali, sebbene preferissero ignorarli, dal momento che per i cenacoli pitagorici era di gran lunga più importante difendere il credo “tutto è numero razionale” piuttosto che concentrarsi sullo studio degli irrazionali, come tuttavia faranno i medio e neo-pitagorici, studi che hanno portato il Professor Antonio Gargano a ravvisare una specie di filiazione tra esiti del neopitagorismo in termini di slancio verso l’ideale e la teoria platonica delle idee, di fatto una filosofia “matematica”.
Quindi, per quanto ignorassero i numeri irrazionali, i Pitagorici avevano, dei numeri, uno spettro abbastanza completo, poiché la scoperta dei radicali apriva loro l’orizzonte vasto dei numeri “reali”.
Vale la pena spendere qualche parola sul credo pitagorico “tutto è numero razionale” che ci servirà poi per capire il concetto di aritmogeometria pitagorica, i suoi sviluppi e la sua applicazione nel campo della cosmologia.
Giamblico nella Vita di Pitagora ci descrive l’atto fondativo del credo pitagorico che avrebbe avuto luogo niente meno che all’interno della bottega di un mastro ferraio. Pitagora era infatti rimasto particolarmente colpito dal fatto che ogni volta che il martello picchiava sull’incudine, alcuni suoni erano consonanti, altri dissonanti. Entrò e fece degli esperimenti accorgendosi che dati due martelli di uguale misura che picchiavano l’incudine, il suono prodotto era ovviamente lo stesso, ma nel momento in cui si utilizzavano due martelli, di cui uno era il doppio dell’altro in termini di peso, il suono era lo stesso, ma l’altezza era diversa. Pitagora scoprì ciò che in musica si chiama intervallo di un’ottava e replicando l’esperimento con martelli il cui rapporto era 3:2, cioè 1,5, ossia un martello pesante una volta e mezzo l’altro, i suoni erano diversi ed equivalenti al rapporto musicale detto di quinta. Ancora, con martelli il cui rapporto era 4:3, ovvero un martello pari ad una volta e un terzo dell’altro, il suono riproduceva un intervallo di quarta.
Ciò portò Pitagora ad una profonda riflessione. Il fenomeno non poteva essere casuale. Da una parte abbiamo, infatti, i martelli e i loro suoni, quindi il mondo fisico oggettivo e dall’altra ritroviamo la musica, il mondo soggettivo, le arti e l’umanesimo. Che cosa mette in comunicazione questi due mondi? La matematica, i numeri, da cui tutto è numero razionale.
Interessante l’uso dell’aggettivo “razionale”. Ratio in latino vuol dire misura, ordine, rapporto. I numeri razionali sono i numeri che possono essere rappresentati tramite rapporto di interi. Il senso della misura nella stessa estetica greca è correlato al numero, poiché la proporzione è numero. Tutta la realtà per Pitagora risponde ad un ordine matematico e non necessariamente la geometria deve essere esclusa da questo universo, perché i Pitagorici attraverso l’aritmogeometria hanno avvicinato matematica e geometria.
Il numero 1 è un punto. Il 2 una retta, il 3 un triangolo, il 4 un quadrato, il 5 un pentagono ecc, tanto che i Pitagorici parlavano di numeri triangolari, quadrati e pentagonali, costruendo attraverso dei sassolini che chiamavano psefoi, le loro figure. Certamente, rispetto ai moderni matematici, consapevoli che i numeri sono astrazioni, i Pitagorici erano fermamente convinti che i numeri fossero res, attribuendo loro delle proprietà specifiche.
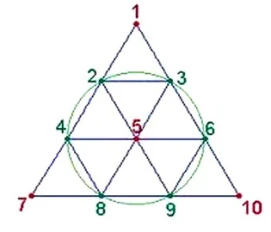
1 è la ragione, 3 è armonia, 10 è la sacra tetraktys perché è duplicazione di 3. Si parte dal vertice, da un triangolo a base 2, a cui viene aggiunta un’ ulteriore sezione a base 3, a cui ne segue un’altra a base 4. Disegnando il tutto con gli psefoi, otteniamo un triangolo al cui interno sono iscritti altri triangoli, dunque un potenziamento del 3, da cui la credenza pitagorica che il 10 fosse la chiave di interpretazione dell’intero universo.
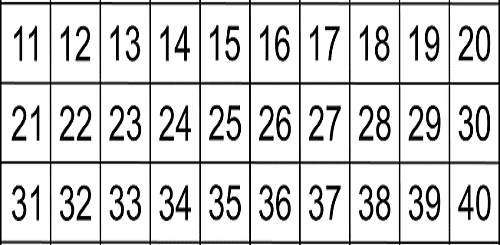
E’ molto importante tuttavia denotare che la numerazione pitagorica partiva proprio dal 3. L’unità è la ragione da cui tutto ha tratto origine per separazione del 2, la diade, ovvero i primi contrari primordiali, pari e dispari, da cui si sarebbero distaccati 9 coppie di opposti. Tutto ciò che si trova sulla linea del dispari è bene e ciò che si trova sulla linea del pari è male.
Strano modo di pensare per noi moderni, ma non per i pitagorici. Rappresentando le figure con gli psefoi, infatti, i pitagorici notarono che tutti i numeri dispari potevano essere disposti in modo e maniera tale da avere un sassolino come vertice di chiusura della figura, a differenza dei pari, che non chiudendo, disegnavano rette estese all’infinito e per la filosofia antica, l’infinito è imperfetto, da cui la credenza che il cosmo, in quanto perfetto, doveva necessariamente essere finito.
1 e 2 entreranno ufficialmente nel sistema dei numeri naturali solo in età post-aristotelica attraverso il logico Crisippo di Soli.
Altre due importanti scoperte pitagoriche in ambito matematico e geometrico sono l’aggiunta di due solidi regolari: dodecaedro e icosaedro, ai precedenti cubo, tetraedro e ottaedro attribuiti agli Egizi e naturalmente la scoperta dell’infinito, cosa che tra l’altro avvenne in modo molto casuale per i Pitagorici, osservando il simbolo, cioè quello che noi moderni chiameremo “logo” della scuola pitagorica, noto come “stella pitagorica”
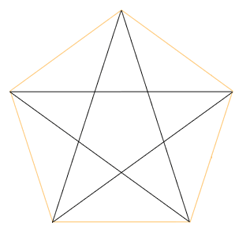
Se inscrivo un pentagono all’interno di un cerchio e traccio le diagonali da ogni angolo del pentagono, al centro ottengo un altro pentagono e dunque potrò tracciare altre diagonali che nel centro mi restituiranno un ulteriore pentagono che mi consentirà di replicare infinite volte l’operazione. Insomma, alla stella pitagorica, viene attribuita la scoperta dell’infinito matematico.
Rimane da trattare ancora un argomento prima di chiudere con la cosmologia: gli irrazionali, che nei manuali di filosofia e di storia della matematica rimandano alla famigerata dimostrazione dell’incommensurabilità della diagonale del quadrato e a ciò che noi oggi chiamiamo sezione aurea.
Cominciamo dal problema della diagonale del quadrato. Dato un quadrato ABCD, tracciando la diagonale BD ottengo un triangolo rettangolo retto in C. Se il quadrato misura 1 di lato, applicando il teorema di Pitagora per calcolare la diagonale ovvero l’ipotenusa del triangolo rettangolo ottenuto, avrò come risultato radice di 2 [fig 3].
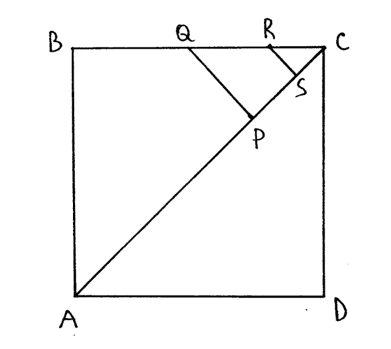
Ebbene, un bravissimo matematico allievo di Pitagora, Ippaso di Metaponto, dimostrò che radice di 2 non è un numero pitagorico rappresentabile come rapporto di numeri interi, ma è un numero irrazionale. Detto in maniera molto semplice – presa una qualsiasi unità di misura, la medesima entrerà un numero “intero” di volte nel lato, ma non rientrerà nella diagonale un numero intero di volte. Dunque, non è possibile misurare allo stesso tempo, con la stessa unità di misura, lato e diagonale.
Per noi parlare di radice di 2 non è qualcosa di così sconvolgente. Tutti quanti, infatti, abbiamo svolto calcoli con i radicali a scuola, ma dobbiamo sempre metterci nei panni degli antichi per capire la portata di certe scoperte.
La dimostrazione per i moderni è ovvia e non abbiamo certo bisogno di ricorrere ad Aristotele che negli Analitici Primi ci ha lasciato una complessissima dimostrazione che chiama in causa il regresso all’infinito. Dalla (2) in figura 3 sappiamo perfettamente che l’identità m2=2n2 è falsa perché, semplicemente, scomponendo in fattori primi, se m2 è un quadrato per via di quell’esponente 2, invece, 2n2, per via di quel 2 davanti ad n2, non darà mai un quadrato, cioè il rapporto di m/n, dove m ed n sono numeri interi, non può restituire radice di 2.
Ciò che per noi è scontato, non fu così indolore per i Pitagorici giacché l’intero sistema filosofico di Pitagora si basava su “tutto è numero razionale”. Perciò, se esistono gli irrazionali, il motto non è vero. La leggenda è poi ben nota. Ad Ippaso venne chiesto di mantenere il silenzio. Ippaso divulgò la notizia e fece una brutta fine. C’è perfino una variante della leggenda secondo la quale i Pitagorici avrebbero addirittura scavato una tomba per Ippaso, quando lo stesso era ancora in vita, come monito al discepolo “disubbidiente”.
Inutile ribadire che per gli storici, la scuola pitagorica non andò in rovina per colpa di Ippaso che rivelò la falla nel sistema pitagorico, ma la reale fine della scuola pitagorica a Crotone fu politica e venne decretata dal demos crotoniate che era evidentemente stufo della continua ingerenza di questi aristocratici pitagorici nelle vicende politiche della città.
Ad Ippaso è legata anche un’altra scoperta nel campo dell’incommensurabile, cioè la sezione aurea, anche se molti studiosi attribuiscono ad Ippaso solo quella della diagonale del quadrato. Comunque, di fatto, è in ambito pitagorico che si deve quest’altra straordinaria scoperta che richiederebbe una trattazione a parte per la complessità.
Che cos’è un rettangolo aureo? E’ un rettangolo in cui il rapporto tra la base e l’altezza è un numero irrazionale 1,6180339887…(i puntini significano altre cifre dopo il 7) normalmente indicato con la lettera greca φ

Dalla figura 4, si denota come φ si ottiene dal rapporto tra la lunghezza maggiore (a) che è medio proporzionale tra la minore b e la somma tra le due (a+b). L’importanza e il mistero della sezione aurea o proporzione divina è la ricorrenza di tale rapporto e della relativa geometria nelle arti figurative fin dai tempi di Fidia, da cui la sezione aurea come «costante di Fidia», fino alla pittura rinascimentale (noto è il caso della «Flagellazione di Cristo» di Piero della Francesca), coinvolgendo perfino il mondo della natura: la traiettoria identificata dal volo di alcuni falchi durante la caccia, o la disposizione dei petali dei fiori a formare la corolla, o ancora, la forma di alcune conchiglie. Veramente interessante il caso della conchiglia. Non è forse negli oceani primordiali che si è costituita la vita sulla Terra? Le conchiglie si trovano proprio nel mare. Può essere tutto una coincidenza?
In ultimo, ma non per ultimo, la famosa serie numerica di Fibonacci che è strettamente correlata alla sezione aurea.
Chiudiamo la nostra trattazione sui Pitagorici con la cosmologia, campo in cui i Pitagorici applicarono l’aritmogeometria del maestro. Come non citare Filolao, pitagorico del V secolo a.C, che anticipò addirittura Copernico! Filolao elaborò una teoria cosmologica, in seguito scartata dal sistema aristotelico-tolemaico, secondo cui al centro dell’universo vi è un fuoco chiamato Hestia, a cui sono attribuite funzioni demiurgiche. Da Hestia si sarebbe poi staccata materia eternamente plasmata che ha preso la forma degli astri.
Intorno ad Hestia si collocano inoltre 9 pianeti, compreso il Sole, e un decimo pianeta chiamato Antiterra per rientrare nel numero sacro 10.
Ecfanto di Siracusa, altro pitagorico, teorizzò per primo il movimento della Terra intorno al suo asse ed Enoclide parlò perfino di “piano dell’eclittica” terrestre, obliquo rispetto all’equatore celeste, fornendo prova di avere già al tempo conoscenze di coordinate geografiche celesti.
Stiamo dunque parlando di conoscenze scientifiche piuttosto avanzate per i tempi, che per quanto avrebbero richiesto Euclide per una prima sistemazione, in campo matematico, tutto questo sapere rivela all’atto pratico una portata molto più complessa di quanto l’aritmogeometria ci potrebbe far pensare a primo impatto.
La matematica pitagorica, insomma era molto più che una semplice conta con i sassolini.